CHEMISTRY STRUCTURE OF ATOM
By SHIVAM MISHRA in 21 Sep 2024 | 05:16 pmKindly help in this problem.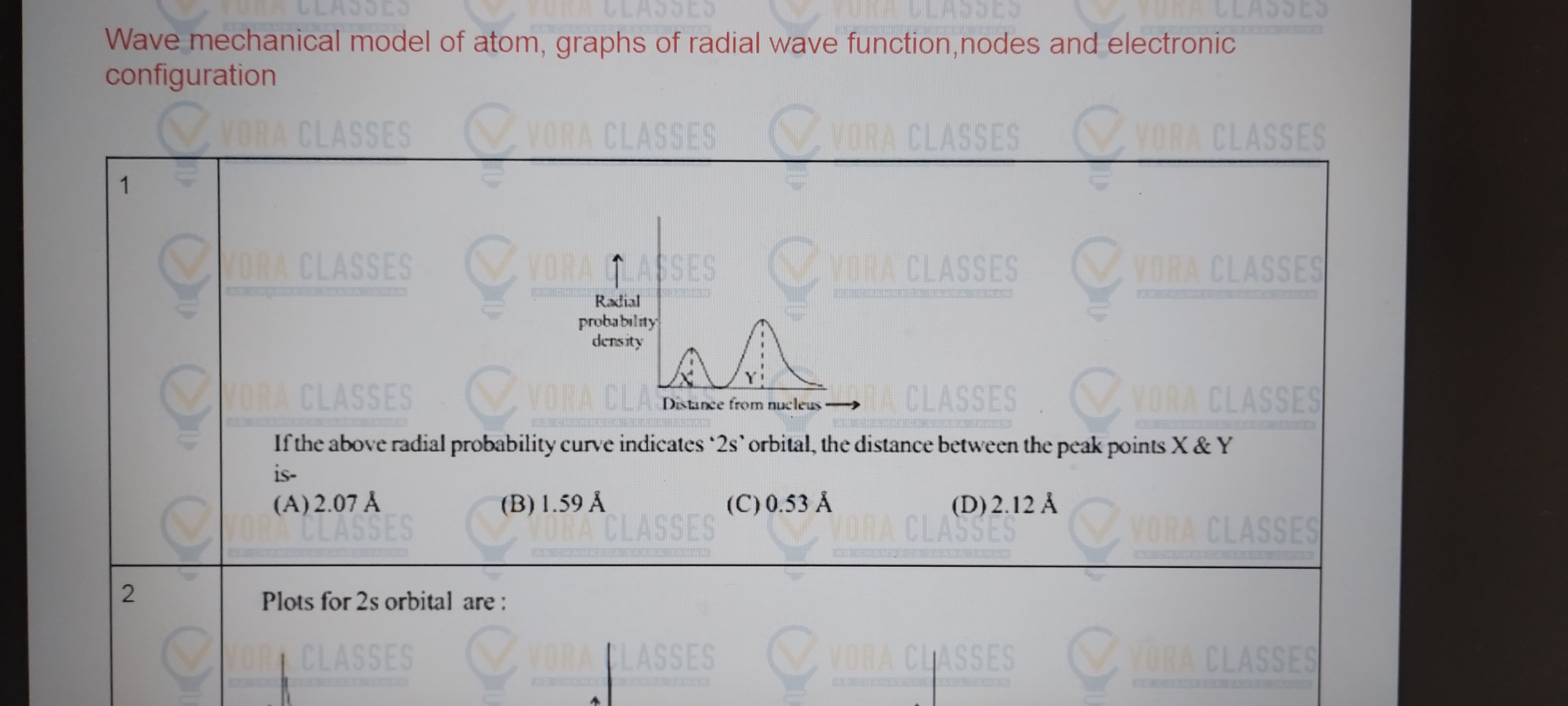
21 Sep 2024 | 05:16 pm
0
Likes
To solve this problem, we need to understand the concept of the radial probability density for the 2s orbital.
The graph provided shows the radial probability density as a function of distance from the nucleus.
Explanation:
- Radial Probability Density:
- Radial probability density is the probability of finding an electron at a certain distance from the nucleus. For the 2s orbital, this graph typically shows two peaks.
- Identifying Peaks:
- In the graph, the peaks are marked as X and Y. These represent the most probable distances from the nucleus where an electron can be found.
- Distance Between Peaks:
- The problem asks for the distance between these two peaks (X and Y).
- Options Analysis:
- You’re given several distances: 2.07 Å, 1.59 Å, 0.53 Å, and 2.12 Å.
- Typically, for the 2s orbital, the distance between the peaks corresponds to a known value based on atomic data.
- Answer:
- For the 2s orbital, the correct distance between the peaks X and Y is usually around 1.59 Å.
Thus, the correct answer is (B) 1.59 Å. This is based on the typical behavior and known data for the 2s orbital in quantum chemistry.
27 Sep 2024 | 12:00 pm
0
Likes

